Análisis de Componentes Principales

Contexto

Una empresa de alimentos está planeando lanzar una campaña de marketing el próximo mes con el objetivo de maximizar las ganancias. En una campaña piloto con 2,240 clientes, aquellos que compraron la oferta fueron etiquetados como exitosos.

Parte 1

Análisis exploratorio 📊

Carga de la base de datos

df <-read.csv("ifood_df.csv")
glimpse(df)

Rows: 2,205
Columns: 39
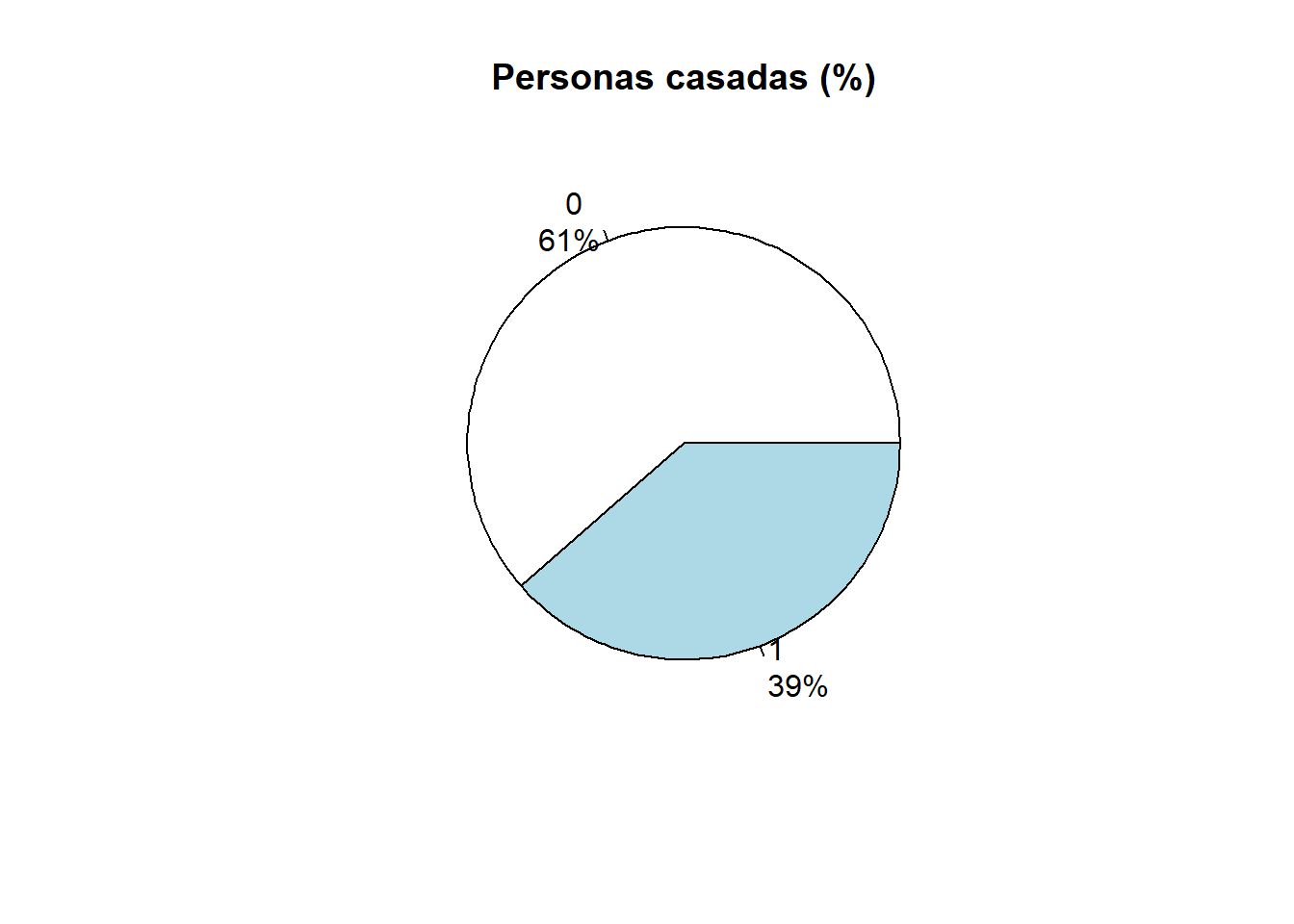
$ Income               <dbl> 58138, 46344, 71613, 26646, 58293, 62513, 55635, …
$ Kidhome              <int> 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0…
$ Teenhome             <int> 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0…
$ Recency              <int> 58, 38, 26, 26, 94, 16, 34, 32, 19, 68, 59, 82, 5…
$ MntWines             <int> 635, 11, 426, 11, 173, 520, 235, 76, 14, 28, 6, 1…
$ MntFruits            <int> 88, 1, 49, 4, 43, 42, 65, 10, 0, 0, 16, 61, 2, 14…
$ MntMeatProducts      <int> 546, 6, 127, 20, 118, 98, 164, 56, 24, 6, 11, 480…
$ MntFishProducts      <int> 172, 2, 111, 10, 46, 0, 50, 3, 3, 1, 11, 225, 3, …
$ MntSweetProducts     <int> 88, 1, 21, 3, 27, 42, 49, 1, 3, 1, 1, 112, 5, 1, …
$ MntGoldProds         <int> 88, 6, 42, 5, 15, 14, 27, 23, 2, 13, 16, 30, 14, …
$ NumDealsPurchases    <int> 3, 2, 1, 2, 5, 2, 4, 2, 1, 1, 1, 1, 3, 1, 1, 3, 2…
$ NumWebPurchases      <int> 8, 1, 8, 2, 5, 6, 7, 4, 3, 1, 2, 3, 6, 1, 7, 3, 4…
$ NumCatalogPurchases  <int> 10, 1, 2, 0, 3, 4, 3, 0, 0, 0, 0, 4, 1, 0, 6, 0, …
$ NumStorePurchases    <int> 4, 2, 10, 4, 6, 10, 7, 4, 2, 0, 3, 8, 5, 3, 12, 3…
$ NumWebVisitsMonth    <int> 7, 5, 4, 6, 5, 6, 6, 8, 9, 20, 8, 2, 6, 8, 3, 8, …
$ AcceptedCmp3         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0…
$ AcceptedCmp4         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ AcceptedCmp5         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0…
$ AcceptedCmp1         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0…
$ AcceptedCmp2         <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ Complain             <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ Z_CostContact        <int> 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3…
$ Z_Revenue            <int> 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 11, 1…
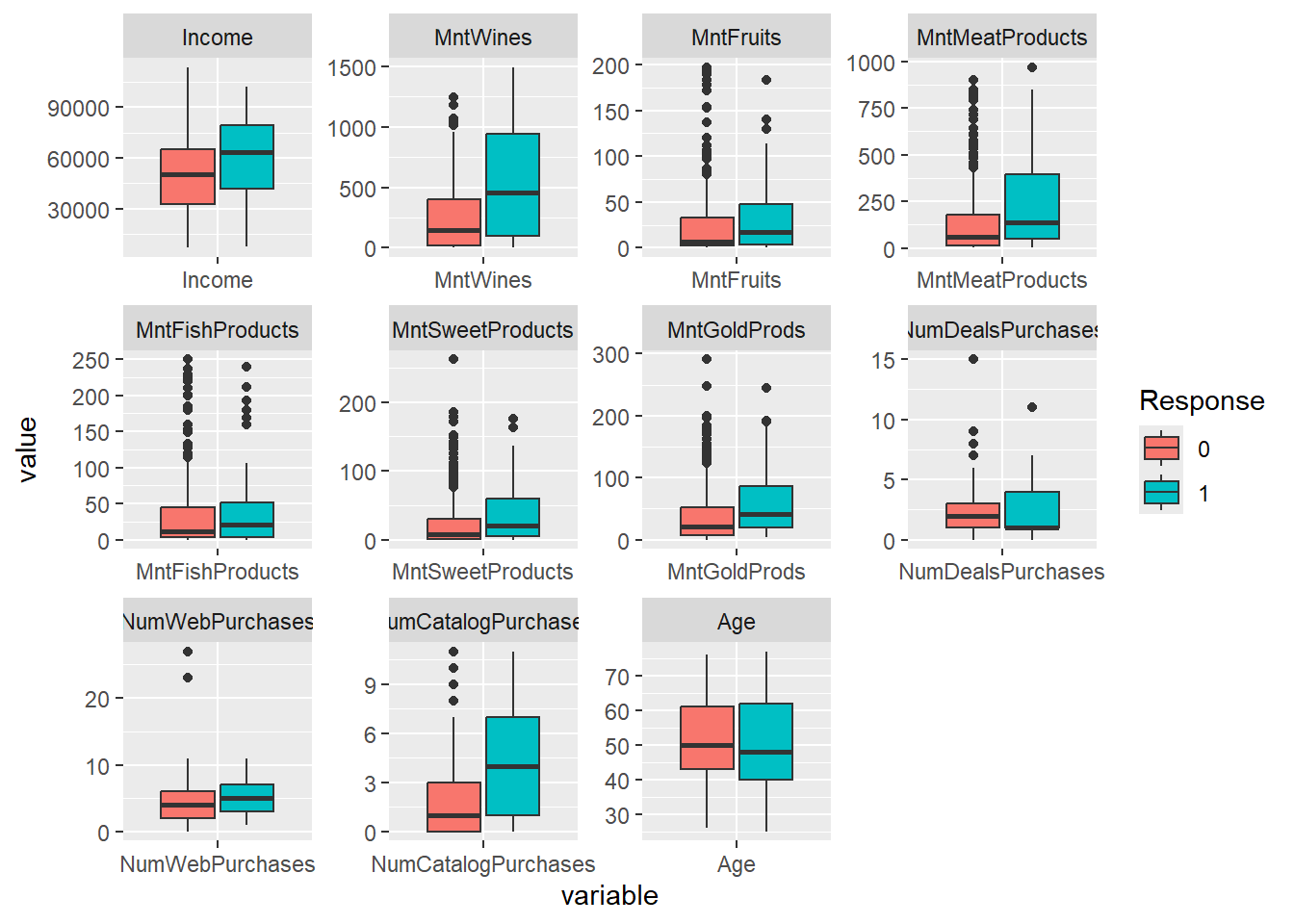
$ Response             <int> 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0…
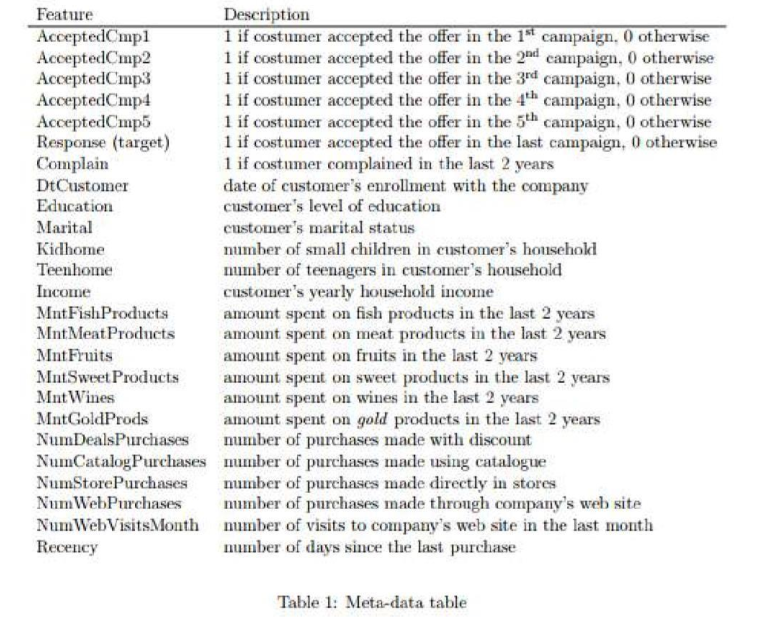
$ Age                  <int> 63, 66, 55, 36, 39, 53, 49, 35, 46, 70, 44, 61, 6…
$ Customer_Days        <int> 2822, 2272, 2471, 2298, 2320, 2452, 2752, 2576, 2…
$ marital_Divorced     <int> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0…
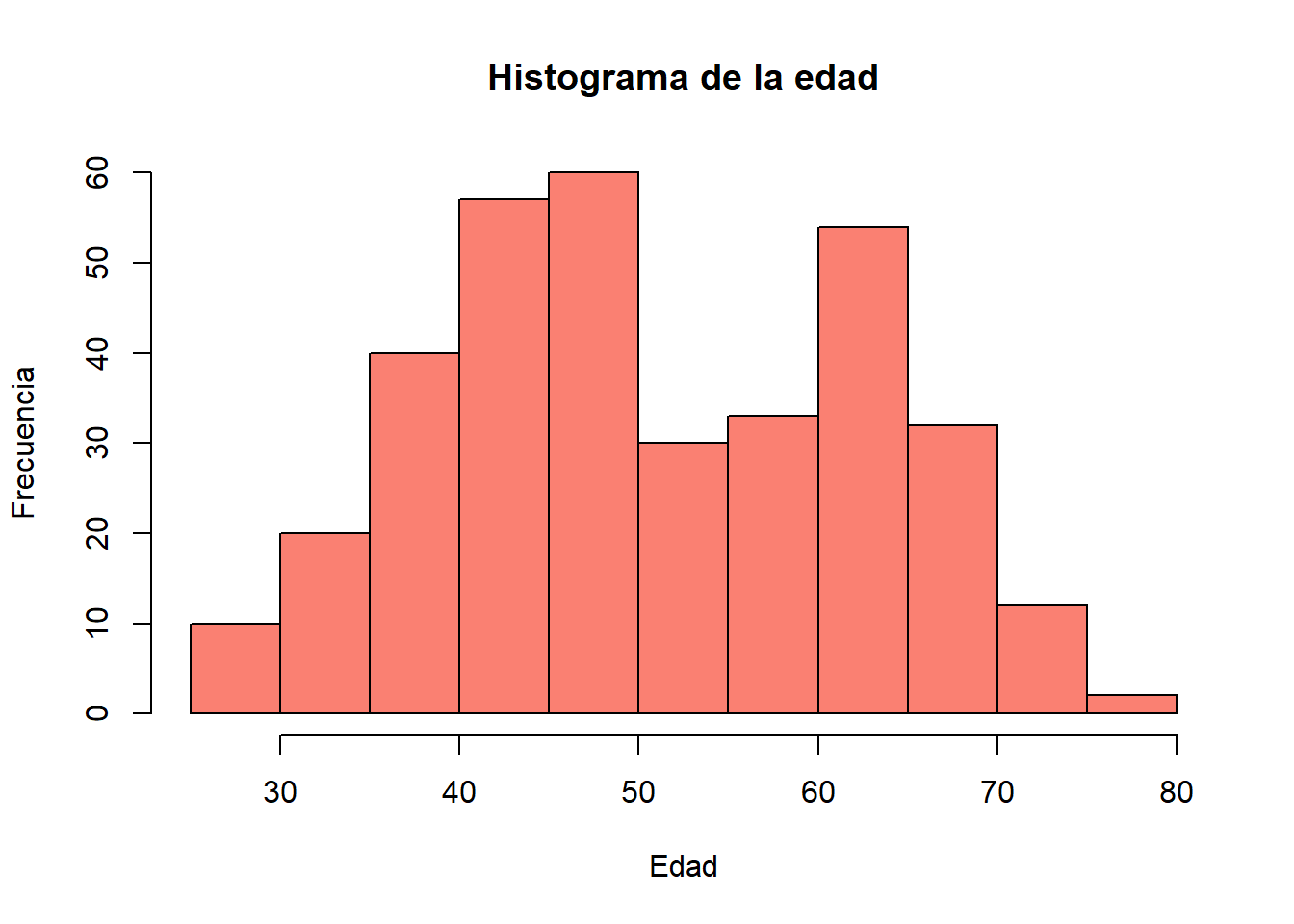
$ marital_Married      <int> 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0…
$ marital_Single       <int> 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0…
$ marital_Together     <int> 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1…
$ marital_Widow        <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ education_2n.Cycle   <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ education_Basic      <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0…
$ education_Graduation <int> 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1…
$ education_Master     <int> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0…
$ education_PhD        <int> 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0…
$ MntTotal             <int> 1529, 21, 734, 48, 407, 702, 563, 146, 44, 36, 45…
$ MntRegularProds      <int> 1441, 15, 692, 43, 392, 688, 536, 123, 42, 23, 29…
$ AcceptedCmpOverall   <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 0…

Descripción de las columnas del dataset

¿Hay valores faltantes?

sum(is.na(df))# para saber cuantos na hay en la base de datos

[1] 0

¿Hay datos duplicados?

any(duplicated(df))

[1] TRUE

set.seed(11) 

df_sample <- dplyr::distinct(df) |> #elimino datos repetidos
           sample_n(350)

df_num <- df_sample |> 
          select(1, 5:13, 25)#selecciono columnas de interes 

df_sample$marital_Single <- as.factor(df_sample$marital_Single)
df_sample$marital_Married <- as.factor(df_sample$marital_Married)
df_sample$Response <- as.factor(df_sample$Response)

hist(df_sample$Age, 
     main = "Histograma de la edad",
     xlab = "Edad",
     ylab = "Frecuencia",
     col = "salmon",
     border = "black"
)

recuentos <- table(df_sample$marital_Married)

# Calcular los porcentajes
porcentajes <- round(prop.table(recuentos) * 100)

# Crear las etiquetas con las categorías y los porcentajes
etiquetas <- paste(names(recuentos),"  \n", porcentajes, "%", sep = "")

# Crear el gráfico de torta con las etiquetas de categorías y porcentajes
pie(recuentos, labels = etiquetas, main="Personas casadas (%)")

# scatter plot

ggplot(df_sample, aes(x=MntWines, y=Income)) + 
  geom_point( colour='#56B4E9', shape=19)+
  xlab("Cantidad de vinos comprados")+
  ylab("Income")+
  theme_bw()

Trabajamos unicamente con las variables numéricas.

data_long <- df_sample |> 
             select(1, 5:13,24, 25) |> 
             melt()
ggplot(data_long, aes(x=variable, y=value)) + 
    geom_boxplot() +
    facet_wrap(~variable, scale="free")

ggplot(data_long, aes(x=variable, y=value, fill= Response)) + 
    geom_boxplot() +
    facet_wrap(~variable, scale="free")

Representación tridimensional de variables

scatter3D(df_sample$MntWines, df_sample$NumWebPurchases, df_sample$Age, 
          phi = 0, 
          bty = "g",
          pch = 20, 
          cex = 2, 
          ticktype = "detailed", 
          colvar=NULL, 
          col = "blue",
          xlab="MntWines",
          ylab="NumWebPurchases",
          zlab="Age")

mycolors <- c('royalblue1', 'red')
df_sample$color <- mycolors[ as.numeric(df_sample$Response) ]

plot3d(df_sample$MntWines, df_sample$NumWebPurchases, df_sample$Age, 
          type = 's', 
          radius = 10,
          col = df_sample$color,
          xlab="MntWines",
          ylab="NumWebPurchases",
          zlab="Age")

rglwidget()

Correlograma

#Matriz de correlación
library(corrplot)

m_cor <- cor(df_num) 

# representa la matriz de correlaciones mediante círculos
corrplot(m_cor,
         method="circle",
         type = "upper",
         diag= FALSE) 

Matriz de Varianzas y covarianzas

m_cov <-round(cov(df_num),2)

m_cov

                          Income   MntWines MntFruits MntMeatProducts
Income              470239182.17 5318804.21 473340.02      2957426.60
MntWines              5318804.21  115736.90   5438.31        41006.64
MntFruits              473340.02    5438.31   1545.12         4398.62
MntMeatProducts       2957426.60   41006.64   4398.62        40859.24
MntFishProducts        611365.94    6710.43   1145.97         6093.56
MntSweetProducts       543070.79    5205.24    959.17         3979.91
MntGoldProds           433362.33    7539.71    718.46         3942.80
NumDealsPurchases       -7429.41      -8.01    -11.89          -68.25
NumWebPurchases         32218.35     492.77     31.78          160.13
NumCatalogPurchases     42875.30     644.80     55.14          354.96
Age                     60083.48     854.98     20.07           95.76
                    MntFishProducts MntSweetProducts MntGoldProds
Income                    611365.94        543070.79    433362.33
MntWines                    6710.43          5205.24      7539.71
MntFruits                   1145.97           959.17       718.46
MntMeatProducts             6093.56          3979.91      3942.80
MntFishProducts             2873.51          1140.71       981.31
MntSweetProducts            1140.71          1612.44       551.77
MntGoldProds                 981.31           551.77      2556.11
NumDealsPurchases            -11.92           -11.85         8.36
NumWebPurchases               39.77            47.12        71.71
NumCatalogPurchases           82.83            57.84        64.80
Age                           11.94            -6.15        27.60
                    NumDealsPurchases NumWebPurchases NumCatalogPurchases
Income                       -7429.41        32218.35            42875.30
MntWines                        -8.01          492.77              644.80
MntFruits                      -11.89           31.78               55.14
MntMeatProducts                -68.25          160.13              354.96
MntFishProducts                -11.92           39.77               82.83
MntSweetProducts               -11.85           47.12               57.84
MntGoldProds                     8.36           71.71               64.80
NumDealsPurchases                3.18            1.20               -0.48
NumWebPurchases                  1.20            9.46                2.87
NumCatalogPurchases             -0.48            2.87                7.62
Age                              1.43            8.18                3.35
                         Age
Income              60083.48
MntWines              854.98
MntFruits              20.07
MntMeatProducts        95.76
MntFishProducts        11.94
MntSweetProducts       -6.15
MntGoldProds           27.60
NumDealsPurchases       1.43
NumWebPurchases         8.18
NumCatalogPurchases     3.35
Age                   135.83

Las varianzas tienen distintas unidades: No son comparables!!

Y la traza??

traza_cov  <-sum(diag(m_cov))
traza_cov

[1] 470404522

La función eigen() calcula los autovectores y autovalores y los almacena en una lista bajo el nombre de vectors y values, respectivamente.

m_cov_AA <- eigen(m_cov)
autovalores_cov <- m_cov_AA$values #autovalores
round(autovalores_cov, 2)

 [1] 470320263.16     57363.48     21059.21      2442.43      1673.67
 [6]      1003.64       586.51       118.31         6.14         2.74
[11]         2.29

Y si estandarizo los datos?

datos_estandarizados <- data.frame(scale(df_num))

#calculo la matriz de covarianzas en los datos estandarizados
round(cov(datos_estandarizados),2)

                    Income MntWines MntFruits MntMeatProducts MntFishProducts
Income                1.00     0.72      0.56            0.67            0.53
MntWines              0.72     1.00      0.41            0.60            0.37
MntFruits             0.56     0.41      1.00            0.55            0.54
MntMeatProducts       0.67     0.60      0.55            1.00            0.56
MntFishProducts       0.53     0.37      0.54            0.56            1.00
MntSweetProducts      0.62     0.38      0.61            0.49            0.53
MntGoldProds          0.40     0.44      0.36            0.39            0.36
NumDealsPurchases    -0.19    -0.01     -0.17           -0.19           -0.12
NumWebPurchases       0.48     0.47      0.26            0.26            0.24
NumCatalogPurchases   0.72     0.69      0.51            0.64            0.56
Age                   0.24     0.22      0.04            0.04            0.02
                    MntSweetProducts MntGoldProds NumDealsPurchases
Income                          0.62         0.40             -0.19
MntWines                        0.38         0.44             -0.01
MntFruits                       0.61         0.36             -0.17
MntMeatProducts                 0.49         0.39             -0.19
MntFishProducts                 0.53         0.36             -0.12
MntSweetProducts                1.00         0.27             -0.17
MntGoldProds                    0.27         1.00              0.09
NumDealsPurchases              -0.17         0.09              1.00
NumWebPurchases                 0.38         0.46              0.22
NumCatalogPurchases             0.52         0.46             -0.10
Age                            -0.01         0.05              0.07
                    NumWebPurchases NumCatalogPurchases   Age
Income                         0.48                0.72  0.24
MntWines                       0.47                0.69  0.22
MntFruits                      0.26                0.51  0.04
MntMeatProducts                0.26                0.64  0.04
MntFishProducts                0.24                0.56  0.02
MntSweetProducts               0.38                0.52 -0.01
MntGoldProds                   0.46                0.46  0.05
NumDealsPurchases              0.22               -0.10  0.07
NumWebPurchases                1.00                0.34  0.23
NumCatalogPurchases            0.34                1.00  0.10
Age                            0.23                0.10  1.00

Matriz de Correlaciones

m_cor <-round(cor(df_num),2)
m_cor |> knitr::kable(format = "html") |> 
  kable_styling() 

	Income	MntWines	MntFruits	MntMeatProducts	MntFishProducts	MntSweetProducts	MntGoldProds	NumDealsPurchases	NumWebPurchases	NumCatalogPurchases	Age
Income	1.00	0.72	0.56	0.67	0.53	0.62	0.40	-0.19	0.48	0.72	0.24
MntWines	0.72	1.00	0.41	0.60	0.37	0.38	0.44	-0.01	0.47	0.69	0.22
MntFruits	0.56	0.41	1.00	0.55	0.54	0.61	0.36	-0.17	0.26	0.51	0.04
MntMeatProducts	0.67	0.60	0.55	1.00	0.56	0.49	0.39	-0.19	0.26	0.64	0.04
MntFishProducts	0.53	0.37	0.54	0.56	1.00	0.53	0.36	-0.12	0.24	0.56	0.02
MntSweetProducts	0.62	0.38	0.61	0.49	0.53	1.00	0.27	-0.17	0.38	0.52	-0.01
MntGoldProds	0.40	0.44	0.36	0.39	0.36	0.27	1.00	0.09	0.46	0.46	0.05
NumDealsPurchases	-0.19	-0.01	-0.17	-0.19	-0.12	-0.17	0.09	1.00	0.22	-0.10	0.07
NumWebPurchases	0.48	0.47	0.26	0.26	0.24	0.38	0.46	0.22	1.00	0.34	0.23
NumCatalogPurchases	0.72	0.69	0.51	0.64	0.56	0.52	0.46	-0.10	0.34	1.00	0.10
Age	0.24	0.22	0.04	0.04	0.02	-0.01	0.05	0.07	0.23	0.10	1.00

Y la traza?

traza_cor  <-sum(diag(m_cor))
traza_cor

[1] 11

Traza = p (número de variables)

desc_mat_cor <-eigen(m_cor)
autovalores_cor <-desc_mat_cor$values
round(autovalores_cor,2)

 [1] 4.97 1.46 1.01 0.75 0.64 0.61 0.46 0.37 0.31 0.23 0.19

print(sum(round(autovalores_cor,2)))

[1] 11

print(sum(round(autovalores_cov, 2)))

[1] 470404522

Conclusión:la suma de los autovalores de cada matriz coincide con su respectiva traza

¿Que matriz usar para extraer a los componentes?

Matriz de varianzas y covarianzas

• Cuando las variables están en la misma escala

• Da más peso a las variables con mayor varianza

• En la interpretación interesa la diferencia entre varianzas

Matriz de correlación:

• Cuando las variables están en distintas escalas o con valores muy distintos

• Da el mismo peso a todas las variables

PCA

Objetivo del PCA

Reducir el número de variables generando nuevas variables que resuman la información original. Revelar patrones en los datos que pueden no ser detectados al analizar las variables por separado.

• Reducción de dimensionalidad
• Detección de anomalías
• Decorrelación: Algunos algoritmos de aprendizaje automático tienen dificultades con características altamente correlacionadas. PCA transforma características correlacionadas en componentes no correlacionados, lo que podría ser más fácil para que el algoritmo trabaje con ellas

Por defecto, prcomp() centra las variables para que tengan media cero, pero si se quiere además que su desviación estándar sea de uno, hay que indicar scale = TRUE.

pca <- prcomp(df_num,
              scale = TRUE)# con datos estandarizados
names(pca)

[1] "sdev"     "rotation" "center"   "scale"    "x"       

center:contienen la media de las variables previa estandarización (en la escala original)

scale: contienen desviación típica de las variables previa estandarización (en la escala original)

rotation: contiene los loadings

Cargas o loadings

round(pca$rotation,2) |> knitr::kable(format = "html") |> 
  kable_styling() 

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	PC10	PC11
Income	0.39	0.01	-0.22	-0.03	0.13	-0.21	0.05	0.02	0.07	-0.12	-0.85
MntWines	0.35	0.20	-0.16	-0.40	0.06	-0.30	-0.12	0.02	-0.34	-0.55	0.34
MntFruits	0.33	-0.21	0.09	0.36	-0.13	0.19	-0.69	-0.07	-0.41	0.11	-0.04
MntMeatProducts	0.36	-0.16	-0.03	-0.26	-0.21	-0.10	-0.10	-0.65	0.48	0.19	0.16
MntFishProducts	0.32	-0.20	0.16	0.20	-0.45	0.23	0.64	-0.12	-0.29	-0.19	0.01
MntSweetProducts	0.33	-0.19	0.11	0.53	0.22	-0.23	0.02	0.32	0.48	-0.25	0.27
MntGoldProds	0.27	0.26	0.36	-0.30	0.14	0.70	-0.09	0.17	0.26	-0.17	-0.06
NumDealsPurchases	-0.06	0.60	0.43	0.16	-0.52	-0.34	-0.14	0.03	0.12	-0.05	-0.13
NumWebPurchases	0.25	0.48	0.12	0.26	0.53	-0.04	0.24	-0.34	-0.23	0.33	0.11
NumCatalogPurchases	0.37	-0.01	-0.02	-0.28	-0.16	-0.15	0.10	0.55	-0.07	0.63	0.12
Age	0.08	0.41	-0.75	0.26	-0.26	0.31	-0.02	0.06	0.16	0.01	0.12

contrib <- as.matrix(round(pca$rotation,2))
corrplot(contrib,is.corr=FALSE)

¿Cuál seria la combinación lineal de la primer componente?

\(\ PC1= 0.39*Income+ 0.35*MntWines + 0.33*MntFruits +0.36*MntMeatProducts +0.32*MntFishProducts +0.33*MntSweetProducts +0.27*MntGoldProds- 0.06*NumDealsPurchases+ 0.25*NumWebPurchases+ 0.37*NumCatalogPurchases+ 0.08*Age\)

Y de la segunda componente (PCA 2)??

#loadings

carga1 = data.frame(cbind(X=1:length(df_num),
                          primeracarga=data.frame(pca$rotation)[,1]))
carga2 = data.frame(cbind(X=1:length(df_num),
                          segundacarga=data.frame(pca$rotation)[,2]))
cbind(carga1,carga2)

    X primeracarga  X segundacarga
1   1   0.39496445  1  0.009448456
2   2   0.34774133  2  0.198230197
3   3   0.32643499  3 -0.207109090
4   4   0.35626029  4 -0.161891520
5   5   0.31803419  5 -0.196372090
6   6   0.32583807  6 -0.187463008
7   7   0.26576364  7  0.258851125
8   8  -0.06278940  8  0.595402294
9   9   0.24864230  9  0.478317339
10 10   0.37421028 10 -0.014630566
11 11   0.07650174 11  0.409021727

ggplot(carga1, aes(colnames(df_num) ,primeracarga)) + 
       geom_bar (stat="identity" , 
       position="dodge" ,
       fill ="royalblue" ,
       width =0.5 ) + xlab( 'Variables' ) + ylab('Primera carga' )+ theme(axis.text.x = element_text(angle = 45, hjust = 1))

Autovalores

¿Qué proporción de la variabilidad total es explicada por las componentes?

pca$sdev^2 # autovalores

 [1] 4.9658092 1.4612271 1.0130561 0.7508607 0.6449025 0.6113400 0.4525177
 [8] 0.3712505 0.3102922 0.2306287 0.1881153

prop_varianza <- pca$sdev^2 / sum(pca$sdev^2)
prop_varianza

 [1] 0.45143720 0.13283883 0.09209601 0.06826006 0.05862750 0.05557637
 [7] 0.04113797 0.03375005 0.02820838 0.02096624 0.01710139

ggplot(data = data.frame(prop_varianza, pc = 1:11),
       aes(x = pc, y = prop_varianza)) +
  geom_col(width = 0.4) +
  scale_y_continuous(limits = c(0,0.15)) +
  theme_bw() +
  labs(x = "Componente principal",
       y = "Prop. de varianza explicada")

prop_varianza <- pca$sdev^2 / sum(pca$sdev^2)
prop_varianza_acum <- cumsum(prop_varianza)
prop_varianza_acum

 [1] 0.4514372 0.5842760 0.6763720 0.7446321 0.8032596 0.8588360 0.8999739
 [8] 0.9337240 0.9619324 0.9828986 1.0000000

ggplot(data = data.frame(prop_varianza_acum, pc = 1:11),
       aes(x = pc, y = prop_varianza_acum, group = 1)) +
  geom_point() +
  geom_line() +
  theme_bw() +
  labs(x = "Componente principal",
       y = "Prop. varianza explicada acumulada")

¿Cuántas CPs elegir?

Criterio 1: Porcentaje de variabilidad explicada

Se define un porcentaje de variabilidad mínimo que se desea explicar y se toman las primeras m componentes que alcanzan este porcentaje de explicación.

Por ejemplo se elige un porcentaje de 80% de variabilidad.

round(prop_varianza_acum*100,2)# llevo datos a porcentaje

 [1]  45.14  58.43  67.64  74.46  80.33  85.88  90.00  93.37  96.19  98.29
[11] 100.00

Criterio 2: Criterio de Kaiser

Consiste en retener las m primeras componentes tales que sus autovalores resulten iguales o mayores que 1.

screeplot(pca, type = "l", npcs = 11)
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"),
       col=c("red"), lty=5, cex=0.6)

Criterio 3: Criterio del bastón roto

Si la proporción de variabilidad explicada por \(Y1, Y2, · · ·, Ym\) se estabiliza a partir de un cierto valor de CP, entonces aumentar la dimensión no aportaría cambios significativos.

library(factoextra)

fviz_eig(pca, ncp =11, addlabels = TRUE, main="")

Parte 2

Vizualización

• Los objetos son ordenados en función de su puntaje en cada uno de los componentes analizados

• Las variables son representadas como vectores

Scores

Se estandarizan las variables originales y luego con la fórmula de la combinación lineal correspondiente para cada CP, se calculan los scores o puntajes de los vinos.

pca$x[,1]# scores para la primer componente (PC1)

  [1] -0.31513875 -1.76272897 -0.03804857 -2.36685863  1.93057658 -2.42723189
  [7]  3.85935893 -2.18355304 -1.55038991 -1.96741912 -2.25446966  3.03307385
 [13] -2.35483581  1.53693354 -1.02432923 -1.88845301 -1.34154434  2.27366105
 [19]  4.71101899 -0.89580185 -0.85406256 -1.41133814  1.78297481 -1.29415617
 [25] -2.11359632 -2.65805478 -0.48089340  0.55921707  2.70343651 -0.03986431
 [31] -2.00854844 -2.38618010 -0.87995910  2.89866257 -1.91906437 -2.43107311
 [37]  0.68502947 -2.08286873  3.71783721  2.31854046 -2.05683411  1.04651983
 [43] -0.13770735 -0.52267892 -1.38354099 -1.17964567 -2.56356035  3.39880778
 [49] -0.02262398  2.47140991  1.66646527  2.57199048 -1.97658382  1.45100330
 [55] -1.87079589  1.69240856 -2.34420602  0.26716479  1.77545615 -1.15129044
 [61] -1.69529920  0.30431248 -2.22581254  1.99149543  3.75939774  3.65451961
 [67]  2.15602746  2.19468564 -2.29766896 -2.45861036  0.33003010 -1.29797246
 [73] -2.13181323 -2.43943037 -2.33245385 -2.03167527 -2.06289552  2.20570590
 [79] -0.64590441 -1.61976519  3.65133496 -1.05922638 -0.92399459 -2.13963600
 [85] -2.18151646 -2.06713181  5.36979559 -0.03956346 -1.64729869 -2.21254736
 [91]  2.10037051 -2.31558002 -1.86722660  2.20841883  1.01315962  0.43694099
 [97]  2.11459312  0.27526943 -2.03238659 -1.64587341  4.08274668 -2.05739673
[103] -1.53647059 -2.31948758 -1.98322526 -1.22708355 -2.02717751 -2.25015292
[109]  2.87853594 -0.43226757  3.50948678 -2.09393572  4.98066935  4.63628858
[115]  1.16592184  1.08163910 -2.37655648  3.57081853 -2.31289353 -1.24532177
[121] -1.76788026  2.41987676  3.56298420 -0.72501748  3.40999877 -1.66629958
[127] -1.68425266 -2.18045779 -2.72462819 -1.21798825 -2.30552066 -0.70011279
[133]  1.20434510  1.59395556 -2.15168305 -1.89008479  0.22422029 -2.48724592
[139] -2.48728978  1.80404523  2.69947232  4.23125961  0.19776518 -0.09580049
[145] -2.19749906 -1.17212913 -1.62877851  1.46530201  3.67113115  3.65528415
[151] -2.24802153 -1.95632427  0.76645652  2.44567219 -2.26430996 -2.42164859
[157]  0.68847126 -0.69775909 -1.29899947  2.78986295  3.31155429  4.50232240
[163] -0.63893253 -2.22903411  1.31465715 -2.38854153 -1.99901213  2.62548469
[169] -0.14779806  0.36903015  3.65413068  2.73785706  0.24576254  0.72091179
[175] -2.26585876  2.54056205  1.47145031  0.74069757 -2.19301909 -2.35036635
[181]  2.22347013 -0.62842206 -1.14710174  0.39629325 -2.52733134 -2.01786414
[187] -2.10706439  0.01822359  0.75648499 -1.99303960  4.00884026 -2.54092052
[193]  1.13278363  3.10213953  1.19947597  4.13571396 -2.53773836  2.35334659
[199]  0.63841515  1.57826026 -1.28308631 -1.08509901 -1.85349457 -2.58543113
[205]  0.24432401  2.53840926 -2.28798954 -2.51363212  2.31625475 -2.25132490
[211]  3.64877301  1.67111599 -2.31364094  1.81014218 -0.67781268  5.06414128
[217]  3.18195155 -2.23606872 -2.50046865  2.88314539 -1.87689013 -0.98313444
[223]  2.68793761 -1.10388438 -2.37156142 -1.97584276 -0.81404519 -1.25920870
[229]  0.59787062 -2.03412003  2.77066250  4.06603059 -0.46101661 -0.29834472
[235]  1.02501346  2.70662126  2.03540492  0.63131342 -2.44247320  2.49856042
[241] -1.28122678 -2.15565486  1.47413664 -1.86079886 -0.28815888 -2.36926092
[247]  0.72657201 -0.21039850 -2.45197888  5.13073212 -1.47646505 -1.79344467
[253]  0.15375968  2.89082499 -1.87918329  3.32669649 -2.22640119 -2.49566835
[259] -0.14753330  2.21604096  0.72037435  0.32380442 -0.68413541 -1.03062262
[265] -2.67456401 -1.61479449  0.46555250 -1.54875186  1.66184328 -2.20021515
[271] -2.06959794  4.45595743 -2.32878398  1.36221973 -0.99334087  0.91372906
[277] -2.52901827 -2.12780678  5.18941775  4.29305296  0.14471147  0.02344002
[283]  1.52336243  3.40771677 -0.42190820  3.06443431  4.02534712 -2.12695295
[289]  6.33418299 -2.03079198 -2.29310419 -0.53868531  0.60518124  1.66203699
[295] -2.46284771  2.76990082 -2.57552862 -2.73925532  3.18863358  2.17073910
[301]  0.82923148 -2.28172130 -2.22892269 -2.16430230 -1.67493204 -1.77263747
[307] -2.09282429 -0.21833344  4.31362840  2.35536044 -2.42717750 -1.65005560
[313]  5.60851347 -1.40918908  0.87776033  2.01745142 -1.27220045 -2.52124627
[319]  2.06741758  0.98594872  2.68534313 -2.06959794 -0.34850620  0.14470618
[325] -1.67797387 -0.26282378  0.58299194  2.04673999 -1.62275590 -1.32605716
[331] -2.37795022 -2.56766454  1.52727219 -1.15060700 -1.84894851 -2.19236555
[337]  3.27705308 -0.91198534 -2.62518047  2.83820231  2.34051278 -2.22150510
[343] -2.15538635 -0.60030120 -1.07608461 -2.42714991  1.06669468  3.79694617
[349]  1.61771705 -1.14645414

res.ind <- get_pca_ind(pca)
knitr::kable(head(res.ind$coord,10), format = "html") %>% 
  kableExtra::kable_styling() %>%
  kableExtra::scroll_box(width = "100%")

Dim.1	Dim.2	Dim.3	Dim.4	Dim.5	Dim.6	Dim.7	Dim.8	Dim.9	Dim.10	Dim.11
-0.3151388	1.3090221	-0.1864862	0.7567850	-1.2303949	-0.0229160	-0.2327718	0.0528448	-0.2972314	0.4726764	-0.1927151
-1.7627290	-0.0489801	-1.9140185	0.3537689	-0.0479994	0.5136666	0.0777874	0.0075862	0.2621559	-0.1393960	-0.3593253
-0.0380486	-0.1340520	-1.6234145	0.8683021	-0.0794713	0.6600385	0.1772770	-0.1261061	-0.2527235	-0.1775694	-0.8731923
-2.3668586	-0.5207344	1.5264464	-0.1407839	0.1773867	-0.1785377	-0.0617663	-0.2221850	-0.1237718	0.0082696	0.4628087
1.9305766	1.4999179	-1.9713362	-0.5250164	0.8789919	-0.2017893	0.2551772	-0.6733537	-0.8135255	-0.0400857	0.5462331
-2.4272319	-1.5420496	0.9982512	-0.1655058	0.6956929	-0.1424526	-0.1316039	-0.0861942	-0.2804195	0.0091746	0.4733454
3.8593589	-1.2417575	0.5542699	-2.7376746	-0.3090574	-0.5905994	-0.4855727	-1.2935101	0.1722122	0.0393368	-0.0046355
-2.1835530	-0.3452174	0.7414846	0.0779548	0.1158884	-0.4984275	-0.0437238	-0.2256860	-0.0437228	-0.0135996	-0.0153349
-1.5503899	0.5092886	0.3853796	-0.0327107	-0.4061442	-0.2175472	-0.0095268	0.0574645	0.1854622	-0.0733781	-0.4233657
-1.9674191	-0.4202863	1.2213761	0.1089785	-0.1140535	0.2152204	0.0513159	0.4526255	0.3220720	-0.1299946	0.6408962

Biplot ✍🏽

library(ggfortify)

autoplot(pca, 
         data = df_num, 
         loadings = TRUE, 
         loadings.colour = 'black',
         loadings.label = TRUE, 
         loadings.label.size = 5)

df_sample$Response <- as.factor(df_sample$Response)

autoplot(pca, 
         data = df_sample, 
         colour = 'Response',
         loadings = TRUE, 
         loadings.colour = 'black',
         loadings.label = TRUE, 
         loadings.label.size = 5)

Vizualicemos las primeras 3 componentes:

componentes <- pca[["x"]]
componentes <- data.frame(componentes)
componentes = cbind(componentes, df_sample$Response)

titulo = 'Primeras 3 CPs'

fig <- plot_ly(componentes, 
               x = ~PC1, 
               y = ~PC2, 
               z = ~PC3, 
               color = ~df_sample$Response,
               colors = c('#636EFA','#EF553B') ) |> 
   add_markers(size = 12)
 
fig <- fig |> 
  layout(
    title = titulo,
    scene = list(bgcolor = "#f3f2fc")
)

fig

¿Qué información podemos sacar del biplot? 🤔

Tener en cuenta lo siguiente:

• Si se es el/la experto/a de dominio (o se le puede consultar) se puede dar una interpretación a qué aspecto del tema se refiere PC1 y PC2, considerando los loadings de las varibles originales.

• Si dos variables forman ángulos pequeños; esto nos estaría diciendo que las variables están muy correlacionadas (en este ejemplo sería el caso de NumCatalogPurchases y Income)

• Si dos variables forman ángulos de 90°, entonces nos indica que ambas variables no están correlacionadas (por ejemplo MntWines y NumDealsPurchases).

• Los resultados del PCA son sensibles a la presencia de outliers por lo que pueden distorsionar el ordenamiento.

¿Y si se quiere graficar el PC2 vs PC3?

autoplot(pca, x = 2, y = 3,
         data = df_num, 
         loadings = TRUE, 
         loadings.colour = 'blue',
         loadings.label = TRUE, 
         loadings.label.size = 4)

library(FactoMineR)
num.pca <- PCA(df_num,              
               scale.unit= TRUE,
               ncp=6,
               graph = FALSE)
names(num.pca)

[1] "eig"  "var"  "ind"  "svd"  "call"

num.pca$eig

        eigenvalue percentage of variance cumulative percentage of variance
comp 1   4.9658092              45.143720                          45.14372
comp 2   1.4612271              13.283883                          58.42760
comp 3   1.0130561               9.209601                          67.63720
comp 4   0.7508607               6.826006                          74.46321
comp 5   0.6449025               5.862750                          80.32596
comp 6   0.6113400               5.557637                          85.88360
comp 7   0.4525177               4.113797                          89.99739
comp 8   0.3712505               3.375005                          93.37240
comp 9   0.3102922               2.820838                          96.19324
comp 10  0.2306287               2.096624                          98.28986
comp 11  0.1881153               1.710139                         100.00000

# Default plot
fviz_pca_ind(num.pca, 
             label="none")

fviz_pca_biplot(num.pca, 
  habillage = df_sample$Response, 
  col.var = "red", 
  label = "var") +
  scale_color_brewer(palette="Dark2")+
  theme_minimal()

Consideraciones importantes 💡

✔️ No es una técnica de inferencia estadística

✔️ El PCA es mas eficiente si las variables se relacionan linealmente.

✔️ Outliers pueden distorsionar el ordenamiento.

PCA robusto 💪🏽

Técnicas robustas

Una de las alternativas robustas propuestas es Minimun Covariance Determinant (MCD), y otra es el Minimum volume ellipsoid (MVE).

Para mas detalle de cada técnica mirar los papers correspondientes:

1- Link de descarga aqui para MCD

2- Link de descarga aquí para MVE.

Se agregan outliers a la base de datos

df_out<-rbind(c (5000, 8000, 3, 100, 20, 300, 5, 10, 150, 10, 81) ,
              c (100000, 9000, 3, 1000, 20, 200, 500, 10, 15, 100, 11) ,
              c (100000, 700, 100, 100, 20, 30, 500, 10, 100, 10, 15),
              df_num)

glimpse(df_out)

Rows: 353
Columns: 11
$ Income              <dbl> 5000, 100000, 100000, 46998, 49389, 70545, 15716, …
$ MntWines            <dbl> 8000, 9000, 700, 172, 40, 138, 16, 997, 1, 1060, 3…
$ MntFruits           <dbl> 3, 3, 100, 41, 0, 39, 5, 26, 12, 61, 3, 1, 3, 0, 8…
$ MntMeatProducts     <dbl> 100, 1000, 100, 86, 19, 63, 30, 269, 9, 835, 31, 4…
$ MntFishProducts     <dbl> 20, 20, 20, 45, 2, 55, 8, 34, 0, 80, 2, 12, 20, 0,…
$ MntSweetProducts    <dbl> 300, 200, 30, 6, 1, 18, 7, 13, 14, 20, 8, 3, 30, 0…
$ MntGoldProds        <dbl> 5, 500, 500, 27, 3, 21, 26, 42, 7, 101, 4, 32, 47,…
$ NumDealsPurchases   <dbl> 10, 10, 10, 5, 1, 1, 3, 1, 1, 1, 3, 4, 3, 3, 1, 1,…
$ NumWebPurchases     <dbl> 150, 15, 100, 5, 2, 4, 3, 10, 2, 4, 3, 3, 2, 3, 3,…
$ NumCatalogPurchases <dbl> 10, 100, 10, 3, 0, 1, 0, 4, 0, 7, 0, 1, 1, 0, 5, 0…
$ Age                 <dbl> 81, 11, 15, 64, 69, 68, 32, 71, 30, 34, 39, 49, 40…

1- Mínimo Determinante de la Covariancia (MCD)

pca_mcd <-princomp(df_out, 
                   cor=TRUE,
                   scores=TRUE,
                   covmat=MASS::cov.mcd(df_out))#se especifica MCD
summary(pca_mcd)

Importance of components:
                          Comp.1    Comp.2    Comp.3     Comp.4     Comp.5
Standard deviation     2.1791297 1.3089245 1.1242006 0.88576719 0.80614342
Proportion of Variance 0.4316915 0.1557530 0.1148934 0.07132577 0.05907884
Cumulative Proportion  0.4316915 0.5874445 0.7023379 0.77366367 0.83274251
                          Comp.6     Comp.7     Comp.8     Comp.9    Comp.10
Standard deviation     0.6837083 0.62790186 0.60584313 0.56073517 0.47827886
Proportion of Variance 0.0424961 0.03584189 0.03336781 0.02858399 0.02079551
Cumulative Proportion  0.8752386 0.91108049 0.94444830 0.97303229 0.99382781
                           Comp.11
Standard deviation     0.260565011
Proportion of Variance 0.006172193
Cumulative Proportion  1.000000000

2- Elipsoide de volumen mínimo (MVE)

Esta estimación busca el elipsoide de volumen mínimo que contiene al menos la mitad de los puntos del conjunto de datos.

pca_mve <-princomp(df_out, 
                   cor=TRUE, 
                   scores=TRUE,
                   covmat=MASS::cov.mve(df_out))#se especifica MVE
summary(pca_mve)

Importance of components:
                          Comp.1    Comp.2    Comp.3     Comp.4     Comp.5
Standard deviation     2.2514814 1.2756411 1.0866953 0.92282280 0.74550914
Proportion of Variance 0.4608335 0.1479327 0.1073552 0.07741836 0.05052581
Cumulative Proportion  0.4608335 0.6087662 0.7161214 0.79353974 0.84406555
                           Comp.6     Comp.7     Comp.8     Comp.9    Comp.10
Standard deviation     0.68987850 0.63904900 0.55756272 0.51126056 0.41996798
Proportion of Variance 0.04326658 0.03712578 0.02826147 0.02376249 0.01603392
Cumulative Proportion  0.88733213 0.92445791 0.95271938 0.97648187 0.99251579
                           Comp.11
Standard deviation     0.286925668
Proportion of Variance 0.007484213
Cumulative Proportion  1.000000000

library(ggpubr)

par(mfrow=c(2,1))
p1 <-fviz_eig(pca_mve, ncp =5, addlabels = TRUE, main="MVE")
p2<- fviz_eig(pca_mcd, ncp =5, addlabels = TRUE, main="MCD")

ggarrange(p1,p2, nrow = 1, ncol = 2)

screeplot(pca_mve, type = "l", npcs = 7)
abline(h = 1, col="red", lty=5)
legend("topright", legend=c("Eigenvalue = 1"),
col=c("red"), lty=5, cex=0.6)

Comparando la varianza explicada entre PCA no robusto y MVE

num.pca.out <- PCA(df_out,              
               scale.unit= TRUE,
               ncp=6,
               graph = FALSE)

fviz_pca_biplot(num.pca.out, 
  col.var = "red", 
  label = "var") +
  scale_color_brewer(palette="Dark2")+
  theme_minimal()

p3 <-fviz_eig(num.pca.out, 
              ncp =5, 
              addlabels = TRUE, 
              main="No robusto",
              barfill = "#69b3a2",
              barcolor = "#69b3a2")

ggarrange(p2,p3, nrow = 1, ncol = 2)

Ejercitación 🤔

La primer componente explica el 29,37% de la variabilidad total de clientes.

Las variables que mas se asocian positivamente con la primer componente son… En cambio, … se asociaron negativamente a la primer componente.

La primer componente diferencia a los vinos tintos de los vinos blancos especialmente referido a los minerales que posee y los sulfitos.

La segunda componente parece captar la variabilidad relacionada con los años en barrica (mayor acidez y alcohol).

sessionInfo()

R version 4.4.1 (2024-06-14 ucrt)
Platform: x86_64-w64-mingw32/x64
Running under: Windows 10 x64 (build 19045)

Matrix products: default


locale:
[1] LC_COLLATE=English_United States.utf8 
[2] LC_CTYPE=English_United States.utf8   
[3] LC_MONETARY=English_United States.utf8
[4] LC_NUMERIC=C                          
[5] LC_TIME=English_United States.utf8    

time zone: America/Buenos_Aires
tzcode source: internal

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] ggpubr_0.6.0     FactoMineR_2.11  ggfortify_0.4.17 factoextra_1.0.7
 [5] corrplot_0.95    kableExtra_1.4.0 plotly_4.10.4    reshape2_1.4.4  
 [9] GGally_2.2.1     plot3D_1.4.1     rgl_1.3.17       gsheet_0.4.6    
[13] ggrepel_0.9.6    lubridate_1.9.3  forcats_1.0.0    stringr_1.5.1   
[17] dplyr_1.1.4      purrr_1.0.2      readr_2.1.5      tidyr_1.3.1     
[21] tibble_3.2.1     ggplot2_3.5.1    tidyverse_2.0.0 

loaded via a namespace (and not attached):
 [1] tidyselect_1.2.1     viridisLite_0.4.2    farver_2.1.2        
 [4] fastmap_1.2.0        lazyeval_0.2.2       digest_0.6.37       
 [7] estimability_1.5.1   timechange_0.3.0     lifecycle_1.0.4     
[10] cluster_2.1.6        multcompView_0.1-10  magrittr_2.0.3      
[13] compiler_4.4.1       rlang_1.1.4          tools_4.4.1         
[16] utf8_1.2.4           yaml_2.3.10          data.table_1.16.2   
[19] knitr_1.48           ggsignif_0.6.4       labeling_0.4.3      
[22] htmlwidgets_1.6.4    scatterplot3d_0.3-44 plyr_1.8.9          
[25] xml2_1.3.6           RColorBrewer_1.1-3   abind_1.4-8         
[28] withr_3.0.1          grid_4.4.1           fansi_1.0.6         
[31] xtable_1.8-4         colorspace_2.1-1     MASS_7.3-60.2       
[34] emmeans_1.10.7       scales_1.3.0         flashClust_1.01-2   
[37] mvtnorm_1.3-3        cli_3.6.3            rmarkdown_2.28      
[40] generics_0.1.3       rstudioapi_0.16.0    httr_1.4.7          
[43] tzdb_0.4.0           base64enc_0.1-3      vctrs_0.6.5         
[46] misc3d_0.9-1         jsonlite_1.8.9       carData_3.0-5       
[49] car_3.1-3            hms_1.1.3            rstatix_0.7.2       
[52] Formula_1.2-5        systemfonts_1.1.0    crosstalk_1.2.1     
[55] glue_1.8.0           ggstats_0.8.0        cowplot_1.1.3       
[58] DT_0.33              stringi_1.8.4        gtable_0.3.5        
[61] munsell_0.5.1        pillar_1.9.0         htmltools_0.5.8.1   
[64] R6_2.5.1             tcltk_4.4.1          lattice_0.22-6      
[67] evaluate_1.0.1       highr_0.11           backports_1.5.0     
[70] leaps_3.2            broom_1.0.7          Rcpp_1.0.13         
[73] svglite_2.1.3        gridExtra_2.3        xfun_0.48           
[76] pkgconfig_2.0.3